Path Differential-Informed Stratified MCMC and Adaptive Forward Path Sampling

Tobias Zirr and Carsten Dachsbacher

ACM Transactions on Graphics, 39, 6, Article 246
Equal-time renderings (50s on 64 cores). Top: We propose a new analytical approach to Markov Chain stratification that improves sample distribution similarly to multi-stage MLT [Hoberock and Hart 2010], but at greatly reduced complexity, as it neither requires multiple rendering stages nor other pre-accumulated information. Bottom: We construct an adaptive rendering algorithm based on purely forward path tracing that is competitive with state-of-the-art bi-directional algorithms. Our analytic variance bounding scheme serves as a framework for the design and optimization of adaptive sampling distributions.
(Scene credits: Kitchen scene by Jay-Artist, prepared by Benedikt Bitterli, and Torus scene by Olesya Jakob, based on a scene by Cline et al. (2005).)

Abstract

Markov Chain Monte Carlo (MCMC) rendering is extensively studied, yet it remains largely unused in practice. We propose solutions to several practicability issues, opening up path space MCMC to become an adaptive sampling framework around established Monte Carlo (MC) techniques. We address non-uniform image quality by deriving an analytic target function for image-space sample stratification. The function is based on a novel connection between variance and path differentials, allowing analytic variance estimates for MC samples, with potential uses in other adaptive algorithms outside MCMC. We simplify these estimates down to simple expressions using only quantities known in any MC renderer. We also address the issue that most existing MCMC renderers rely on bi-directional path tracing and reciprocal transport, which can be too costly and/or too complex in practice. Instead, we apply our theoretical framework to optimize an adaptive MCMC algorithm that only uses forward path construction. Notably, we construct our algorithm by adapting (with minimal changes) a full-featured path tracer into a single-path state space Markov Chain, bridging another gap between MCMC and existing MC techniques.

Downloads

Preprint Supplementary Data (coming soon) Teaser Video Talk TL;DR Slides

Supplementary Data

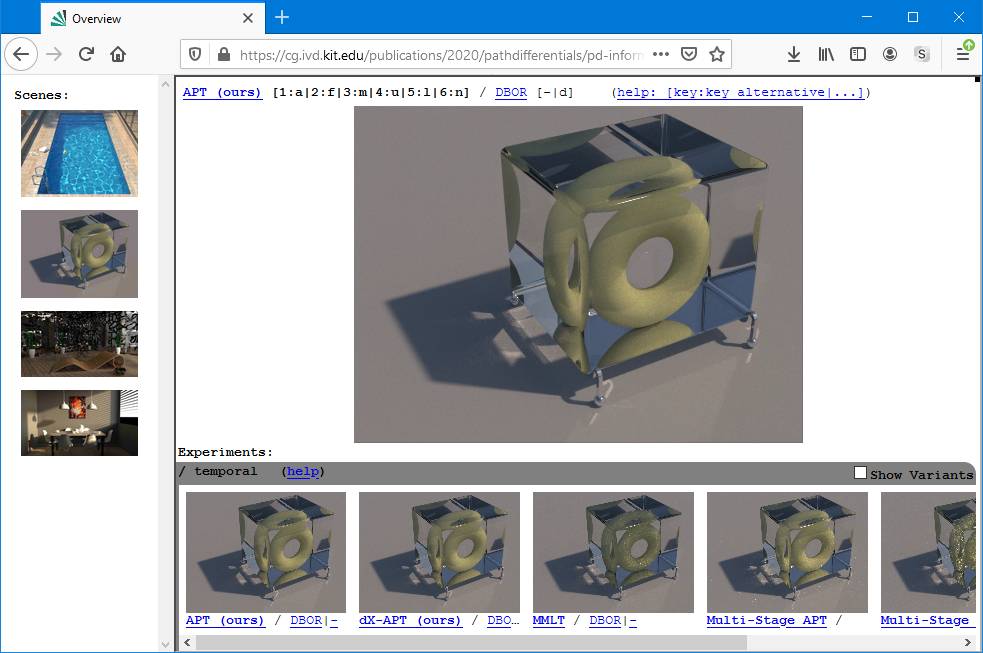
Comparing Temporal Stability for Various MCMC Techniques

Experiments showing 12 independent frames to evaluate temporal stability / consistency of results across multiple runs or in motion. Also shows reweighted results using standard DBOR [DeCoro et al. 2010, Zirr et al. 2018], where the MLT splats were rendered to a cascade of framebuffers and reweighted in post to bound variance.

-: Unbiased Result
DBOR: Standard DBOR applied to each frame individually

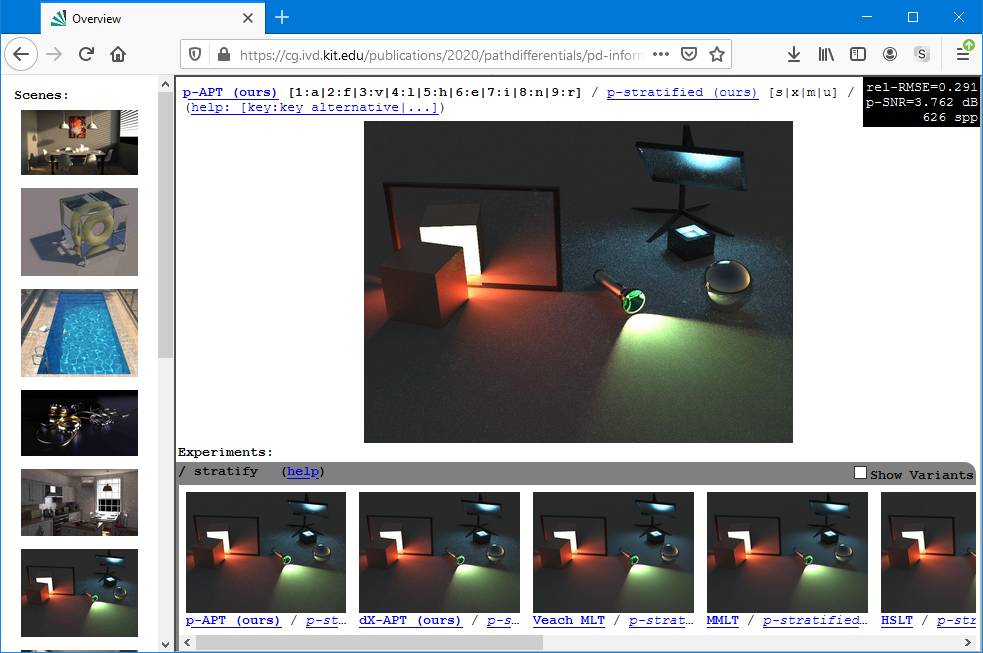
Comparing Stratification for Various MCMC Techniques

Additional results for Fig. 5 (unstratified and stratified MLT, multi-stage MLT)

p-stratified: Simplified stratification based on solid angle PDFs
dX-stratified: Stratification based on fully computed 4D path differentials
multi-stage: Multi-Stage MLT for stratification
unstratified: Using the classic MLT target function

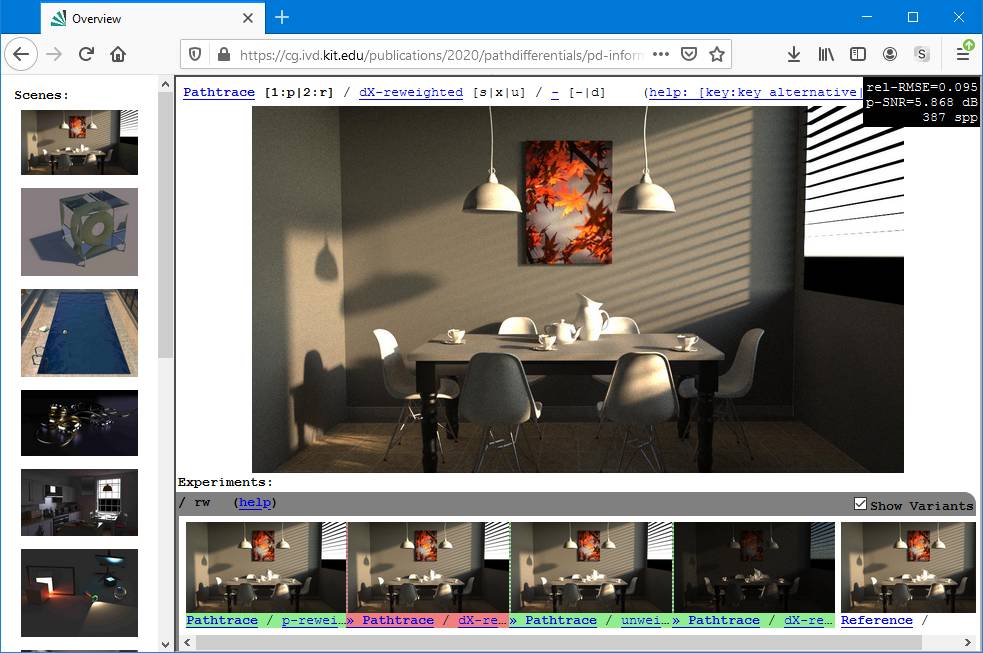
Using Path Differentials for Reweighting / Variance Bounding

Additional results for Fig. 3, using our variance bounding ratio instead of the downweighting ratio derived for DBOR by Zirr et al. [2018]

p-reweighted: Reweighting using the simplified variance bounding ratio
dX-reweighted: Reweighting based on ratio obtained from fully computed 4D path differentials
unweighted: The unbiased result

All images were computed using standard path tracing (no MLT involved)

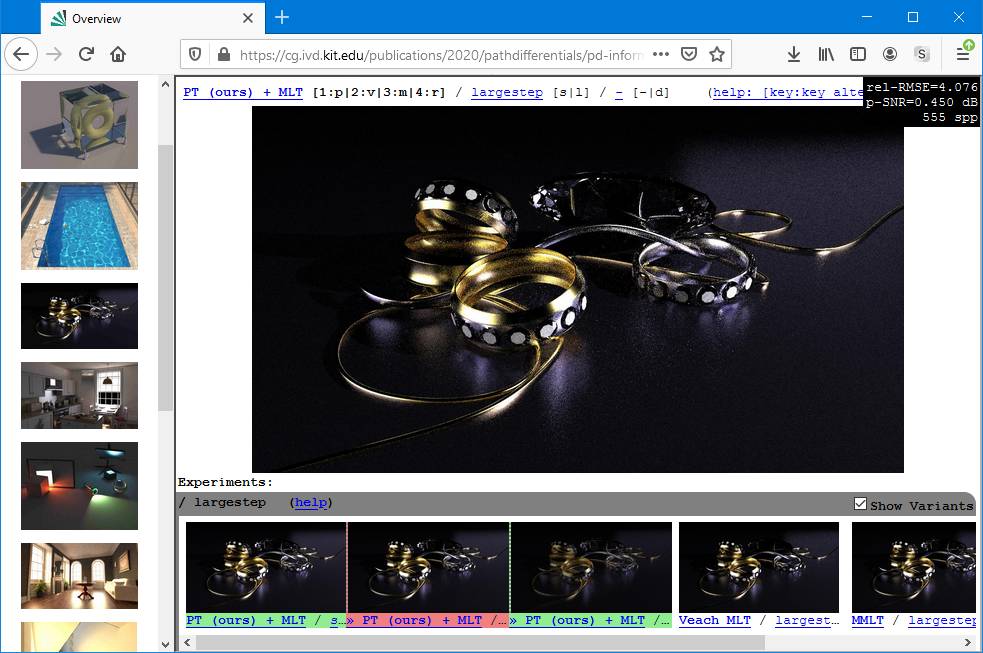
Comparison of Large-Step Mutations in Various MCMC Techniques

Additional results for Fig. 4 (comparing our PT mutation, the bi-directional Mutation in Veach MLT and MMLT large steps, with and w/o the Veach small steps resp. MMLT small steps)

PT + MLT: Our large step, with and w/o lens, caustic and multi-chain perturbations
Veach MLT: Bi-directional mutation, with and w/o lens, caustic and multi-chain perturbations
MMLT: Multiplexed MLT large steps, with and w/o small steps

Amount of Reweighting per Number of Bounces

Shows reweighting experiments separately per number of path bounces, for a simple scene with varying glossinesses. Thus, it becomes visible for which cases the variance bounding is most aggressive.

p-reweighted: Reweighting using the simplified variance bounding ratio
dX-reweighted: Reweighting based on ratio obtained from fully computed 4D path differentials
unweighted: The unbiased result

alpha: Roughness coefficient of a microfacet BRDF Beckmann lobe