Eurographics Symposium on Rendering 2020
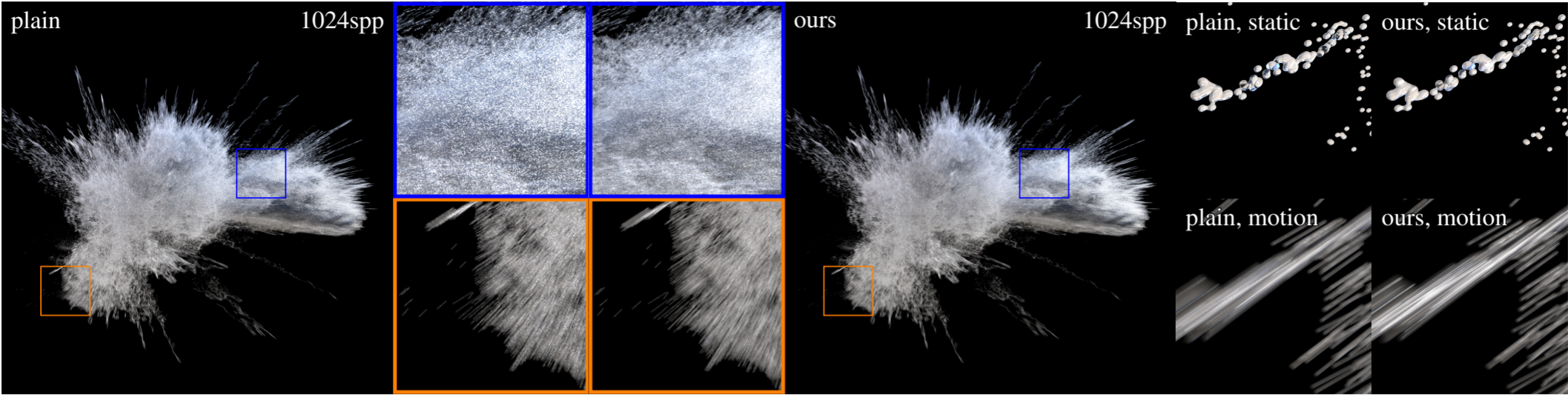
A fast moving water splash, consisting of an isosurface generated by
12M particles. High curvature detail with highly glossy Bidirectional
Scattering Distribution Function (BSDF) creates difficult,
glint-like specular highlights (see details in right images). These are even
harder to sample when the objects are fast moving. Our approach alters the
roughness of the microfacet BSDF specifically to account for motion (compare the static crops
to the right with the moving ones just below),
introducing a temporal normal distribution function. This distribution captures the anisotropic
motion of the highlight and allows us to render such cases efficiently.
Abstract
Specular aliasing can make seemingly simple scenes notoriously hard to render efficiently: small geometric features with high curvature and near specular
reflectance result in tiny lighting features which are difficult to resolve at low sample counts per pixel.
LEAN and LEADR mapping can be used to convert geometric surface detail to anisotropic surface roughness in a preprocess.
In scenes including fluid simulation this problem is particularly apparent with fast moving elements such as spray particles, which are typically represented as participating media in movie rendering.
Both approaches, however, are only valid in the far-field regime where the geometric detail is much smaller than a pixel, while the challenge of resolving highlights remains in the meso-scale.
Fast motion and the relatively long shutter intervals, commonly used in movie production, lead to strong variation of the surface normals
seen under a pixel over time aggravating the problem.
Recent specular anti aliasing approaches preintegrate geometric curvature under the pixel footprint for one specific ray
to achieve noise free images at low sample counts.
We extend these to anisotropic surface roughness and to account for the temporal surface normal variation due to motion blur.
We use temporal derivatives to approximate the distribution of the surface normal seen under a pixel over the course of
the shutter interval.
Furthermore, we discuss how this can afterwards be combined with the surface BSDF in a practical way.
Downloads
Bibtex
@inproceedings{2020_tndf,
author = {Lorenzo Tessari and
Johannes Hanika and
Carsten Dachsbacher and
Marc Droske},
title = {Temporal Normal Distribution Functions},
booktitle = {{EGSR} - Digital Library Only Track},
pages = {1--12},
year = {2020},
doi = {10.2312/sr.20201132}
}